【導讀】對于二階系數(shù),我們將設置電容C2處于其高頻狀態(tài)(以短路代替它),同時我們將確定驅動電感L1的阻抗。圖17說明了這種方法。因為輸出因C2短路,節(jié)點a和c都處于相同的0V電勢。電路簡化為右側示意圖。
06 二階系數(shù)
對于二階系數(shù),我們將設置電容C2處于其高頻狀態(tài)(以短路代替它),同時我們將確定驅動電感L1的阻抗。
圖17說明了這種方法。因為輸出因C2短路,節(jié)點a和c都處于相同的0V電勢。電路簡化為右側示意圖。
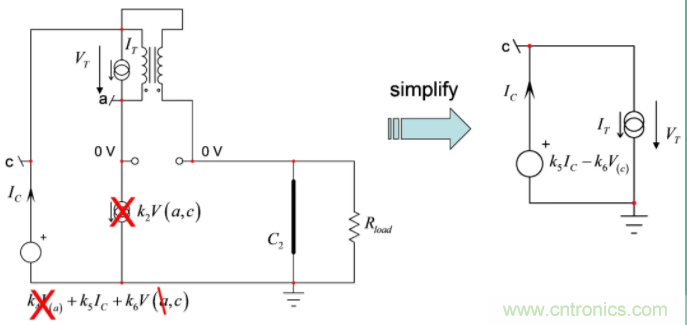
圖17:二階系數(shù)設置儲能元件之一處于其高頻狀態(tài)(C2),同時您可確定電感兩端的電阻。
我們可寫出描述VT電壓的第一個方程。觀察到a) IT和IC是相同的,b) VT = –V(c),我們有
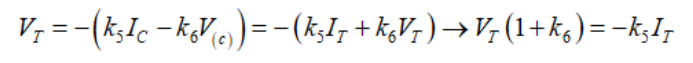 (34)
(34)因式分解VT/IT,L1兩端的阻抗為
二階時間常數(shù)定義為
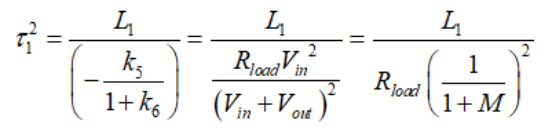 (36)
(36)如果我們認為Vout = MVin,b2系數(shù)表示為
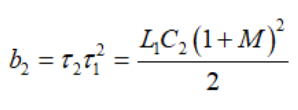 (37)
(37)合并我們確定的時間常數(shù),得出分母D(s)
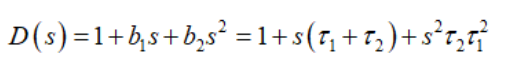 (38)
(38)如果我們考慮一個低Q值的近似值,這二階分母可以近似由兩級聯(lián)極點定義為
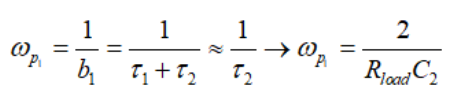 (39)
(39)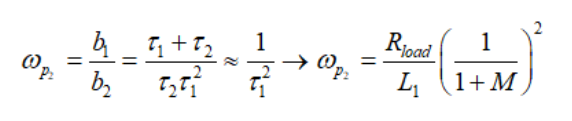 (40)
(40)和合并為
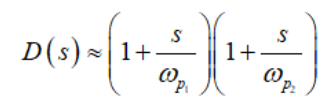 (41)
(41)07 零點的確定
如上文所述,當激勵源調至零角頻率sz,,變形電路的響應為無信號輸出(見圖1)。該運用現(xiàn)將包括將激勵源復原和確定無信號輸出的變形電路的條件。圖18所示為我們需要研究的更新電路。無信號輸出的有趣之處在于其傳播至其它節(jié)點。
例如,如果Vout = 0V,然后由于變壓器高邊連接,節(jié)點a也處于0 V,所有涉及該節(jié)點的表達式可以簡化為如圖所示。如果輸出無信號,則電流I1也為零,這意味著Ic=I3。
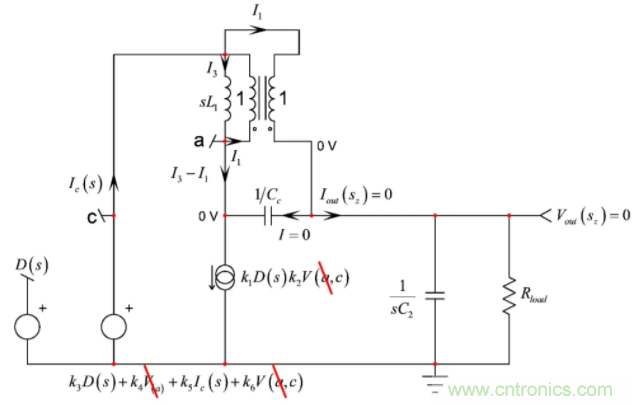
圖18:在s=sz的特定條件下,觀察變形的電路,無信號響應。
節(jié)點c的電壓定義為
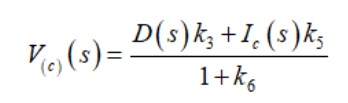 (42)
(42)因此,電流Ic等于節(jié)點c的電壓除以L1的阻抗。
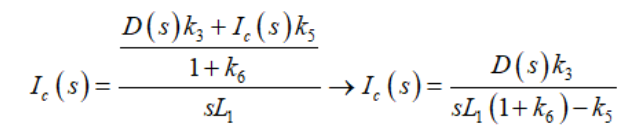 (43)
(43)而電流等于
現(xiàn)將(43)代入(44),然后視Ic=I3:
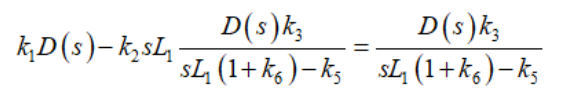 (45)
(45)求解s,將系數(shù)k的值換為它們在圖13中的值,重新整理,您會發(fā)現(xiàn)
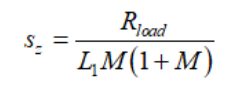 (46)
(46)這是個正的根源,因此為右半平面零點。通過收集所有的部分,發(fā)現(xiàn)極點和零點實際上是一個DCM buck-boost轉換器的極點和零點而得出完整的傳遞函數(shù):
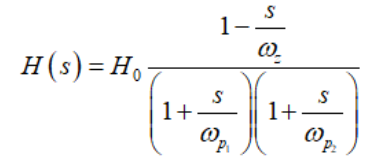 (47)
(47)及
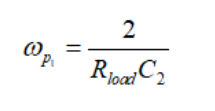 (48)
(48)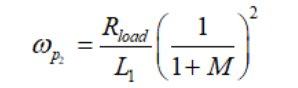 (49)
(49)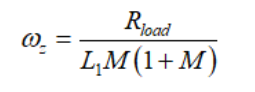 (50)
(50)和
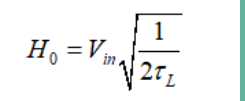 (51)
(51)最后的檢查,我們可比較Mathcad®和圖11大信號模型的SPICE仿真的動態(tài)響應。如圖19所示,曲線完美重合。
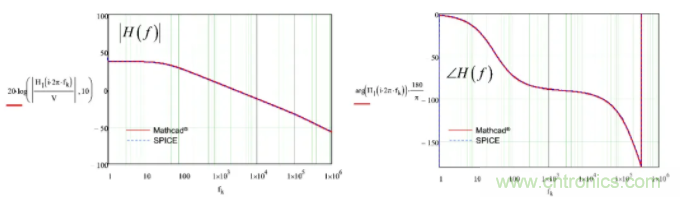
圖19:Mathcad®和SPICE提供完全相同的響應(曲線完美疊加)。
另一個驗證是由采用不同的平均模型(架構如[11])仿真相同的SEPIC結構構建。這也是一個自動切換的CCM-DCM模型,但走線方式稍有不同。圖20所示為兩種平均模型采用一個類似的SEPIC架構。
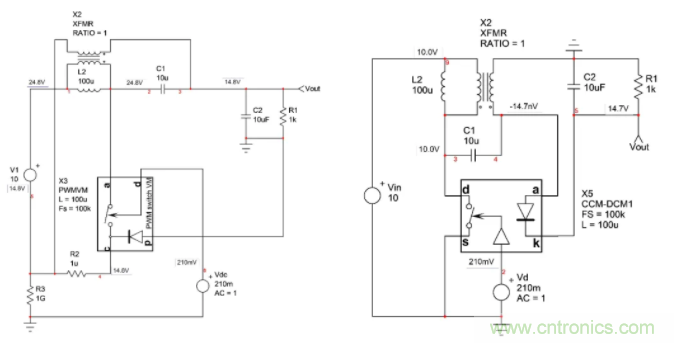
圖20:CoPEC平均模型包括單獨的開關和二極管連接。
圖21證實了兩個交流響應在相位和幅值上完全相同。
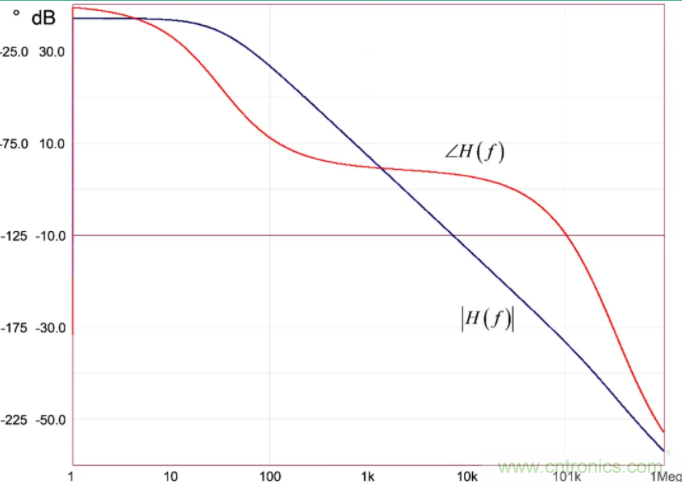
圖21:DCM PWM開關和CoPEC DCM模型提供相同的動態(tài)響應。
08 總結
快速分析技術為推導線性電路傳遞函數(shù)提供了一種快速而高效的方法。在無源電路中,觀察是可能的,而且是經常的,無需寫一行代數(shù)就能得到傳遞函數(shù)。隨著電路變得復雜和包括激勵源,您不得不采用經典的KCL和KVL分析。但當您確定分子和分母中個別的多項式因子時,很容易跟蹤錯誤和只關注錯誤項,如果有的話。在復雜的電路中,小草圖和SPICE的幫助是極有用的。
最后,最終結果以一種有意義的格式表示,并可直接識別出極點和零點位于何處。這是非常重要的,因為您必須知道問題隱藏在傳遞函數(shù)的何處。作為一個設計人員,您必須平衡它們,這樣自然的產生傳播或組件的變化不會危及您的系統(tǒng)在運行中的穩(wěn)定性。
參考文獻
1. R. D. Middlebrook, Methods of Design-Oriented Analysis: Low-Entropy Expressions, Frontiers in Education Conference, Twenty-First Annual conference, Santa-Barbara, 1992.
2. R. D. Middlebrook, Null Double Injection and the Extra Element Theorem, IEEE Transactions on Education, Vol. 32, NO. 3, August 1989.
3. V. Vorpérian, Fast Analytical Techniques for Electrical and Electronic Circuits, Cambridge University Press, 2002.
4. C. Basso, Linear Circuit Transfer Functions – An Introduction to Fast Analytical Techniques, Wiley, 2016.
5. V. Vorpérian, Simplified Analysis of PWM Converters Using the Model of the PWM Switch, Parts I and II, Transactions on Aerospace and Electronics Systems, vol. 26, no. 3, May 1990.
6. D. Feucht, Design-Oriented Circuit Dynamics, http://www.edn.com/electronics-blogs/outside-the-box-/4404226/Design-oriented-circuit-dynamics
7. D. Peter, We Can do Better: A Proven, Intuitive, Efficient and Practical Design-Oriented Circuit Analysis Paradigm is Available, so why aren''t we using it to teach our Students?,
http://www.icee.usm.edu/ICEE/conferences/asee2007/papers/1362_WE_CAN_DO_BETTER__A_PROVEN__INTUITIVE__E.pdf
8. C. Basso, Fast Analytical Techniques at Work with Small-Signal Modeling, APEC Professional Seminar, Long Beach (CA), 2016, http://cbasso.pagesperso-orange.fr/Spice.htm
9. J. Betten, Benefits of a coupled-inductor SEPIC, slyt411, application note, Texas-Instruments.
10. C. Basso, Switch-Mode Power Supplies: SPICE Simulation and Practical Designs, McGraw-Hill, 2nd edition, 2014.
11. D. Maksimovic, R. Erickson, Advances in Averaged Switch Modeling and Simulation, Power Electronic Specialist Conference Professional Seminar, Charleston, 1999
推薦閱讀:






