通過判斷對一個脈沖激勵的響應能否在足夠長的時間內完全衰減為0，可以將濾波器分為無限脈沖響應（IIR）和有限脈沖響應（FIR）兩種。

 

在上世紀初濾波器剛剛問世的時候，其功能主要是通過電子電路的方式的方式實現(xiàn)（電阻、電容以及電感組成的電路，即模擬濾波器）。當時濾波器的使用要求非常高，工程師們不但要有非常深厚的基礎理論知識，更要有足夠的使用經驗，才能正確地設計出合適的濾波器。

 

隨著科技的發(fā)展，尤其是計算機以及各種集成電路的發(fā)展，濾波器技術也越來越成熟，數(shù)字濾波器也隨之出現(xiàn)。這種濾波器使用一系列數(shù)字乘法器、加法器以及時延器來實現(xiàn)對離散信號的濾波功能，在已知傳遞函數(shù)的基礎上，設計出濾波器所需參數(shù)，然后寫入其程序。

 

濾波器的主要功能是為了去除不想要的頻率成分，并且盡可能完整地保留需要的頻率成分?，F(xiàn)今最常用的四種IIR濾波器分別為：巴特沃斯、貝塞爾、切比雪夫和橢圓濾波器。下面將詳細闡述以下這四種濾波器的特點以及區(qū)別。

 

巴特沃斯（Butterworth）濾波器

 

巴特沃斯濾波器首先由英國物理學家Stephen Butterworth于1930年發(fā)明出來。他曾經指出：一個理想的濾波器不應僅僅將不需要的成分剔除，同時也要能夠完整地保留需要的成分。這樣理想的濾波器在理論上本難以實現(xiàn)，但是Butterworth提出，如果使用足夠多合適的元器件將可以無限接近這種理想濾波器的要求。他在論文中指出，如果一個低通濾波器的截止頻率為1rad/s，那么可以將其幅值增益設計為

 

 

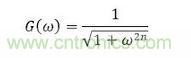
其中ω為角頻率，n為該濾波器的階次。

 

一個這樣的三階濾波器可以如圖示電路實現(xiàn)

 

 

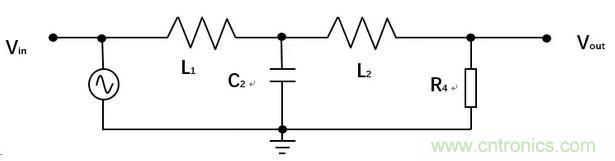
這個電路的傳遞函數(shù)為

 

 

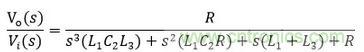
各元器件的值設置如下：C2=4/3 F，R4=1 Ω，L1=3/2 H，L3=1/2 H。所以傳遞函數(shù)可以寫為

 

 

使用jω代替s之后，該傳遞函數(shù)的幅值增益即

 

 

所有的濾波器設計都是在原型濾波器（低通濾波器）的基礎上進行的，將傳遞函數(shù)的s用1/s替換，則可以得到高通濾波器；如果將低通和高通濾波器串聯(lián)即可得到帶通濾波器。N階Butterworth低通濾波器的傳函幅值增益如下

 

 

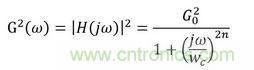
其中n為濾波器階數(shù)；ωc為截止頻率；G0為直流增益，即在頻率零點處的增益，如果是低通的話，一般設置為1。

 

根據(jù)此特性要求，巴特沃斯低通濾波器的傳遞函數(shù)可由Butterworth多項式來實現(xiàn)，即

 

 

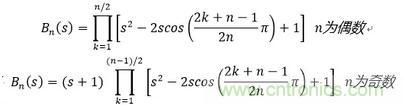
傳遞函數(shù)為

 

 

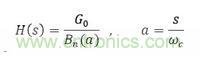
下圖為1階到6階截止頻率為1000Hz的Butterworth低通濾波器的幅值特性曲線

 

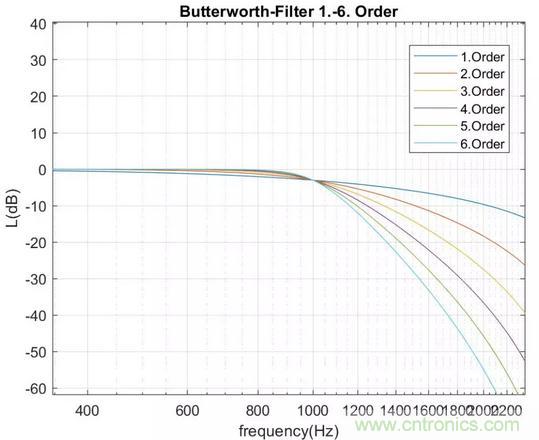
Butterworth低通濾波器

 

由圖可見，階數(shù)越高的濾波器在阻帶的衰減就越快，對于1階濾波器，其衰減速度為-6dB/oct或者-20dB/decade；2階為-12dB/oct，以此類推。當然，階數(shù)越高，所需要的電子元器件也越多，設計越復雜，同時響應特性也越好。

 

貝塞爾（Bessel）濾波器

 

該濾波器的命名來源于德國數(shù)學家Friedrich Bessel。1949年，W. E. Thomson將Bessel函數(shù)成功地應用到濾波器設計上，所以Bessel濾波器也叫作Bessel-Thomson濾波器。同其他的濾波器一樣，Bessel濾波器的原型也是一個低通濾波器，它的傳遞函數(shù)是

 

 

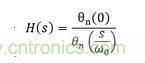
其中θn(s)為反貝塞爾多項式（reverse Bessel polynomial），ω0為截至頻率

 

 

比如一個截止頻率為1rad/s的三階低通濾波器的傳遞函數(shù)為

 

 

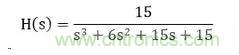
其幅值增益為

 

 

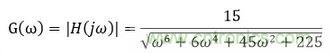
1到6階截止頻率為1000Hz的bessel低通濾波器幅值特性如下圖

 

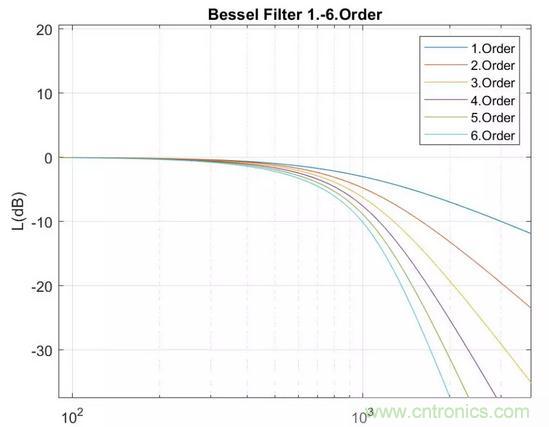
Bessel低通濾波器

 

同Butterworth濾波器一樣，其階數(shù)越高，阻帶衰減也就越快，但是從通帶的幅值響應看來，其保留通帶部分的能力沒有Butterworth濾波器出色。Bessel濾波器具有最平坦的幅度和相位響應。帶通的相位響應近乎呈線性。Bessel濾波器可用于減少所有IIR濾波器固有的非線性相位失真。Bessel線性相位濾波器正是由于具有向其截止頻率以下的所有頻率提供等量延時的特性，才被用于音頻設備中。在音頻設備中，必須在不損害頻帶內多信號的相位關系前提下，消除帶外噪聲。

 

切比雪夫（Chebyshev）濾波器

 

該濾波器根據(jù)俄羅斯數(shù)學家PafnutyChebyshev來命名的，因為設計該濾波器所使用的數(shù)學模型正是基于切比雪夫多項式。該濾波器的特點是過渡帶衰減快，和理想濾波器之間的誤差最小，但是在通帶（Type I）或者阻帶（Type II）存在幅度波動。

 

I型切比雪夫濾波器：

 

這是運用得最多得一種切比雪夫濾波器，其傳遞函數(shù)得幅值增益為

 

 

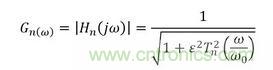
其中ω0是截止頻率；Tn是n階切比雪夫多項式

 

 

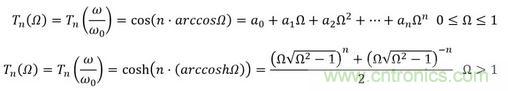
ε是通帶幅度波動因子，它與幅值波動δ之間得關系是

 

 

當ε等于1時，該濾波器得復制波動為3dB。

 

1到6階截止頻率為1000Hz的I型切比雪夫低通濾波器幅值特性如下圖

 

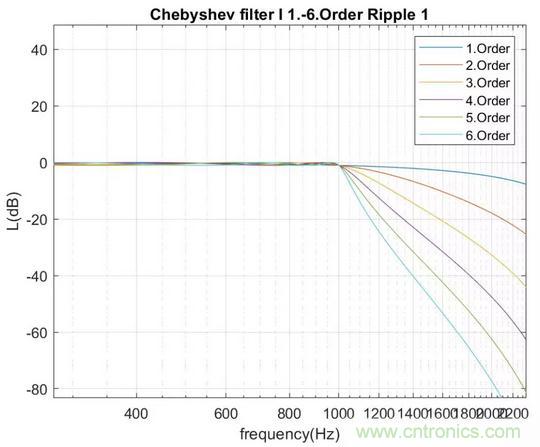
I型切比雪夫低通濾波器

 

II型切比雪夫濾波器：

相較于I型切比雪夫濾波器，II型切比雪夫的應用就要少很多，原因主要有兩點，一是它在過渡帶衰減得沒有I型濾波器快，二是在濾波器的設計上需要更多的元器件。雖然其在通帶不再有幅值波動，但是在阻帶卻出現(xiàn)了等幅值波動，只有在極少數(shù)需要此特性的應用場合才會被使用。其傳遞函數(shù)的的幅值增益為

 

 

1到6階截止頻率為1000Hz的II型切比雪夫低通濾波器幅值特性如下圖

 

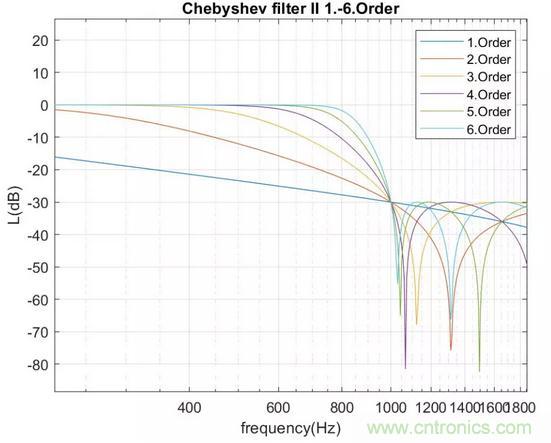
II型切比雪夫低通濾波器

 

橢圓（Elliptic）濾波器

 

橢圓濾波器，有時候也被稱作Cauer濾波器。這種濾波器在通帶和阻帶都帶有等幅值波動，當然在過渡帶的衰減速度也最快。其傳遞函數(shù)為

 

 

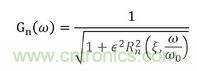
其中，ω0為截止頻率；ε為波動因子；ξ為elliptic rational function的選擇因子，值大于等于1。其中ε的值決定通帶的波動幅值；ε和ξ一起決定阻帶的波動。如果將ξ值設置為∞的話，那么Rn則會變?yōu)榍斜妊┓蚨囗検?，那么該濾波器就變?yōu)榍斜妊┓騃型濾波器了；如果再此基礎上再將ε設為0，使ω0趨近于0，并讓εRn(ξ,1/ω0)=1的話，此濾波器就變?yōu)榘吞匚炙篂V波器；如果其他條件不變，使ξ0ω=α的話，則此濾波器則會變?yōu)榍斜妊┓騃I型濾波器。所以可以說上面的兩種濾波器都可以通過限制橢圓濾波器的某些參數(shù)而得到。但也正因如此，橢圓濾波器的設計較上面的兩種濾波器要復雜一些，應用場合也要少一些。

 

1到6階截止頻率為1000Hz的橢圓低通濾波器幅值特性如下圖

 

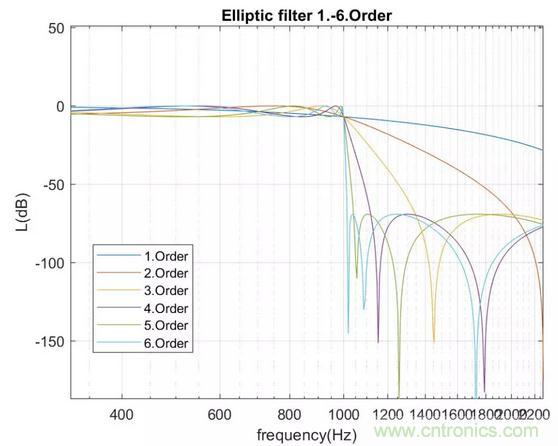
橢圓低通濾波器

 

濾波器對比

 

巴特沃斯濾波器：

使用范圍最廣，因為其完美地保存了通帶內的信號，并且在阻帶內也沒有波動，過度區(qū)域的衰減速度雖然比不上切比雪夫濾波器以及橢圓濾波器，但是也不算最慢；

貝塞爾濾波器：

雖然在通帶和阻帶內都沒有波動，但是保留通帶信號的能力以及過渡帶衰減速度都沒有巴特沃斯卓越；

切比雪夫濾波器：

和理想濾波器的誤差最小，所以應用場合較多，尤其是I型切比雪夫濾波器，如果能夠將其波動因子設置得盡量小的話，其性能甚至比巴特沃斯濾波器要高，但同時也對元器件的要求非常高。

 

下圖為不同的6階低通濾波器的幅值曲線：

 

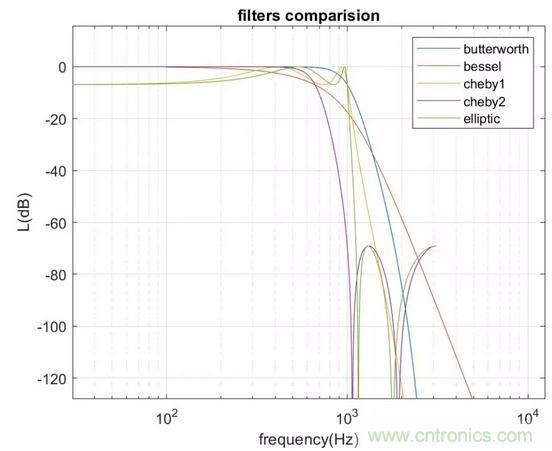
不同濾波器對比

 

ArtemiS SUITE里的IIR濾波器

 

在ArtemiS SUITE的濾波池中可直接調用IIR濾波器，如下圖。

 

 

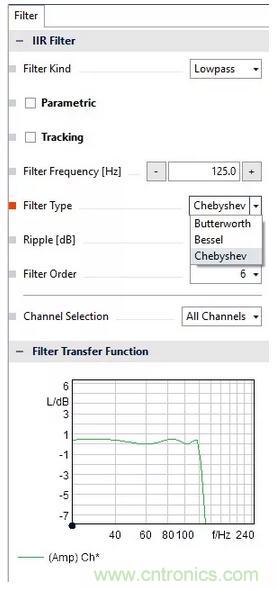
有三種IIR濾波器可供選擇，分別為切比雪夫I型、貝塞爾以及巴特沃斯濾波器。對于不同類型的濾波器可自定義參數(shù)。比如對于巴特沃斯濾波器需要定義截止頻率和濾波器階數(shù)，如果是帶通或者帶阻，還需要確定通帶/阻帶帶寬；如果是切比雪夫濾波器的話，還需要確定波動值。

 

在最下方還可以直觀地看到該濾波器的頻響曲線，使設計濾波器的過程更加直觀準確。

 

當然ArtemiS可以實現(xiàn)的功能不僅僅是這些，如果勾選上Parametric選項的話，它還可以實現(xiàn)參數(shù)濾波器的功能，即原信號其他頻率部分不變，只對感興趣的帶寬內的信號作加強/抑制。（只在highpass，lowpass和bandpass時可選）。

 

除此之外ArtemiS還提供階次跟蹤濾波的功能，軟件將會自動識別所感興趣階次的頻率并進行濾波，在這種情況下將不必自定義截止頻率。

 

來源：海德聲科