【導讀】本文詳細分析設(shè)備中存在的電磁干擾,首先采用盒狀設(shè)計方法,要求箱體表面縫隙的直線尺寸要小于干擾電磁波波長的1/4,箱體的通風孔設(shè)計成波導管的形狀,對欲屏蔽的電磁波構(gòu)成衰減。然后,通過軟件仿真得到箱體屏蔽效能曲線和數(shù)據(jù),根據(jù)仿真結(jié)果優(yōu)化箱體結(jié)構(gòu)設(shè)計。最后,對設(shè)備進行EMI輻射測量,實測數(shù)據(jù)未超過GJB151A-97 RE102限值,驗證設(shè)備箱體的EMI屏蔽設(shè)計達到了設(shè)計要求。
0 引言
箱體屏蔽是抑制電磁干擾(EMI)的重要手段,主要針對輻射的電磁干擾進行抑制。對于裝在箱體內(nèi)的電子學系統(tǒng)來說,該系統(tǒng)運行過程中需要通風散熱,要顯示電壓電流值、顯示運行狀態(tài),那么通風孔、安裝表計及外部連接器需要在鋼板上開孔,箱體上留下縫隙,就會破壞完整的密封屏蔽,由此引起的屏蔽性能的下降。通過設(shè)備箱體的屏蔽設(shè)計,提高設(shè)備的屏蔽性能,要求設(shè)備箱體抑制EMI能力達到GJB151A-97 RE102標準限值。
1 屏蔽技術(shù)分析
屏蔽是以某種導電材料或?qū)Т挪牧现瞥傻钠帘误w將敏感器件或區(qū)域封閉起來,形成電磁隔離,達到阻斷或減少電磁能傳播的一種技術(shù),是抑制電磁干擾的措施之一。屏蔽抑制的是以場的形式沿空間傳播的干擾,它是一種雙向抑制的技術(shù),既可以限制內(nèi)部輻射的電磁能量泄漏,又可以防止外部輻射干擾進入。
電磁屏蔽按其屏蔽原理可分為:
1)電場屏蔽,包含靜電屏蔽和交變電場屏蔽;
2)磁場屏蔽,磁場屏蔽包含低頻磁場屏蔽和高頻磁場屏蔽;
3)電磁場屏蔽,既是前兩種的總和。
1.1 電磁干擾的屏蔽效能
屏蔽效能是用來描述屏蔽體的好壞的指標。它表現(xiàn)了屏蔽體對電磁波的衰減程度。由于屏蔽體通常能將電磁波的強度衰減到原來的1/100至1/10000,因此通常用分貝來表述 。
。
設(shè)備箱體的屏蔽效能計算示意圖如圖1所示。
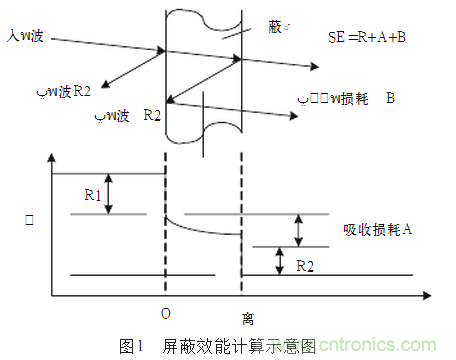
1)設(shè)備箱體的屏蔽材料吸收部分電磁波,形成吸收損耗;
2)電磁波在設(shè)備箱體內(nèi)發(fā)生反射,減小了電磁波的強度。反射后衰減的電磁波稱為反射損耗。
根據(jù)SE=R+A+B
其中,SE為屏蔽效能,A為吸收損耗,R為反射損耗,B為多次反射損耗。
上式中
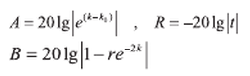
出于分析的角度,利用式(1)來計算位吸收損耗:
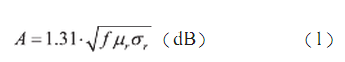
式中f為頻率(Hz), 為屏蔽體材料相對于銅的相對磁導率、
為屏蔽體材料相對于銅的相對磁導率、 為屏蔽體材料相對于銅的相對電導率,
為屏蔽體材料相對于銅的相對電導率,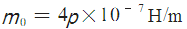 為常數(shù)
為常數(shù)
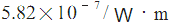 為常數(shù),l為壁厚(cm)。
為常數(shù),l為壁厚(cm)。
1.2 箱體屏蔽材料的特性及其結(jié)構(gòu)選擇
由磁屏蔽理論可知,磁屏蔽是利用由高導磁材料制成的磁屏蔽體來構(gòu)成的,提供低磁阻的磁通路使得大部分磁通在磁屏蔽體上來分流,達到屏蔽的目的。磁導率成為選擇磁屏蔽材料的主要依據(jù)。
通常磁性材料分為:
1)弱磁性材料,包括順磁性物質(zhì)和抗磁性物質(zhì),其特點是相對磁導率產(chǎn) =1,B與H是線性關(guān)系,
=1,B與H是線性關(guān)系, 在任意頻率的環(huán)境中,始終保持常數(shù);
在任意頻率的環(huán)境中,始終保持常數(shù);
2)強磁性材料:鐵磁性物質(zhì),其特點是B與H為非線性關(guān)系,頻率增高,磁導率 降低。
降低。
屏蔽效能除了與屏蔽材料直接相關(guān)外,與屏蔽體結(jié)構(gòu)也相關(guān)。
電屏蔽結(jié)構(gòu),影響電屏蔽的一個重要的因素就是分布電容C,減小C就能提高屏蔽效能。因此一般情況下,電屏蔽體的形狀最好設(shè)計成盒形,盒形結(jié)構(gòu)通常包括單層蓋結(jié)構(gòu)盒雙層蓋結(jié)構(gòu),根據(jù)要求屏蔽的程度不同來選擇。
磁屏蔽結(jié)構(gòu),磁屏蔽是利用屏蔽體對磁通進行分流,因而大多采用盒狀、筒狀或柱狀的結(jié)構(gòu)。由于磁阻與磁路的橫截面積?和磁導率成反比,因而磁屏蔽體的體積和重量都比較大。若要求較高的屏效時,一般采用雙層屏蔽,此時在體積重量增加不多的情況下,能顯著提高屏蔽效能。
電磁屏蔽結(jié)構(gòu),電磁屏蔽是利用屏蔽體對干擾電磁波的吸收、反射來達到減弱干擾能量作用的。因此,電磁屏蔽可采用板狀、盒狀、筒狀、柱狀的屏蔽體。
1.3 不完整屏蔽對屏蔽效果的影響
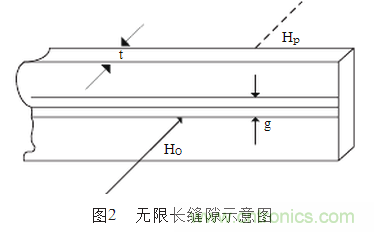
1.3.1 縫隙影響
如圖2所示,設(shè)在金屬屏蔽體中有一無限長的縫隙,其間隙距離為g,屏蔽板的厚度為t,入射電磁波的磁場強度為H0,泄漏到屏蔽體中的磁場強度為Hp,當趨膚深度d>0.3g?時,可以得到 。由上式分析可以知道,當縫隙較窄較深時(亦即t較大,g較小),磁場泄漏就小,反之就大。磁場通過這個縫隙的衰減為
。由上式分析可以知道,當縫隙較窄較深時(亦即t較大,g較小),磁場泄漏就小,反之就大。磁場通過這個縫隙的衰減為
(2)只是對實際情況的簡化和抽象,縫隙所帶來的泄漏比較復(fù)雜,它與縫隙的寬度、板材的厚度,縫隙的數(shù)目以及波長等都有密切關(guān)系。干擾的頻率越高,縫隙的泄漏越嚴重,特別是當縫隙的直線尺寸接近波長時,會產(chǎn)生天線效應(yīng),嚴重地破壞屏蔽體的屏蔽效果。
1.3.2 通孔影響
由于通風及其安裝固定各種附件的需要,可能會在在屏蔽結(jié)構(gòu)上開有圓形或矩形的孔洞,電磁波會通過這些孔洞產(chǎn)生泄漏。
設(shè)屏蔽板上有若干個孔洞,包括圓孔和方孔,孔的面積為S,屏蔽板面積為A,當A遠大于S的時候,亦即圓孔的直徑或方孔的邊長比波長小很多時,通過孔洞泄漏的磁場強度Hp為
若屏蔽板上有n個孔,則總的泄漏磁場強度為
若孔為矩形,其短邊為a,長邊為b,曲積為S'',設(shè)與矩形孔泄漏等效的圓孔面積為S,則:
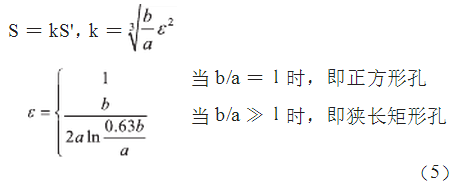
結(jié)合上述幾個公式可得泄漏磁場強度。
在實際情況下,金屬屏蔽板后側(cè)電磁波總的透射系數(shù)應(yīng)為金屬屏蔽板本身的透射系數(shù)TS與孔洞電磁波的透射系數(shù)之和,即
其中
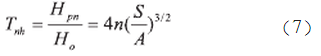
因此總的屏蔽效能為
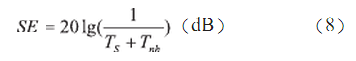
2 屏蔽體通風孔的結(jié)構(gòu)設(shè)計
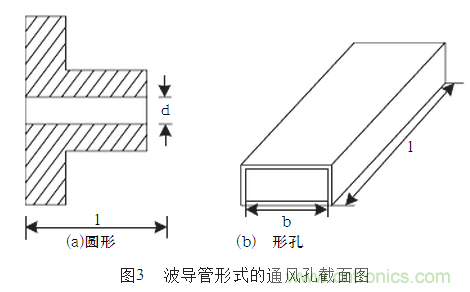
合理的結(jié)構(gòu)設(shè)計,可以使屏蔽體在開了若干通風孔以后,不但能保證良好的通風散熱,而且能保證屏蔽效能不下降,其基本出發(fā)點在于,將每個通風孔設(shè)計成對欲屏蔽的電磁波構(gòu)成衰減波導管的形狀 ,如圖3所示。
,如圖3所示。
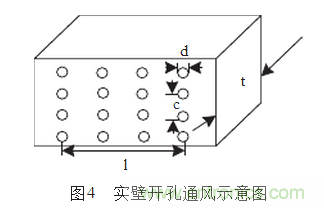
2.1 箱體通風窗的實壁結(jié)構(gòu)設(shè)計
通用通風窗結(jié)構(gòu)是直接在屏蔽體壁上開孔,如圖4所示。每個通風孔直徑為d,相鄰?fù)L孔間矩為d,相鄰?fù)L孔間矩為c,通風孔形成的通風窗口(孔陳列)的邊長為l,屏蔽壁厚為t,則該窗口對磁場的總屏蔽效能為
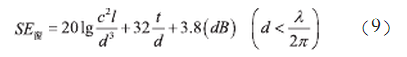
2.2 箱體通風窗的蜂窩結(jié)構(gòu)設(shè)計
設(shè)備箱體的實壁開孔結(jié)構(gòu)設(shè)計,對于電磁屏蔽存在兩個問題:
1)實壁開孔結(jié)構(gòu)設(shè)計要滿足形成衰減器的條件,要求t大于d,即要求箱體的壁厚大于開孔的孔徑。要求孔徑小于l/4;
2)如果在設(shè)備箱體上直接開通風孔,那么灰塵會通過通風孔進入箱體內(nèi),污染電子學系統(tǒng),甚至可能導致短路現(xiàn)象的發(fā)生。蜂窩結(jié)構(gòu)設(shè)計的通風窗可以避免此類現(xiàn)象的發(fā)生。
綜合上述兩種原因,本設(shè)備箱體選擇蜂窩結(jié)構(gòu)的通風窗設(shè)計,達到良好的屏蔽效果。
2.3 箱體結(jié)構(gòu)優(yōu)化設(shè)計
針為避免設(shè)備箱體內(nèi)的電子學系統(tǒng)的元器件工作時溫度高,必須在箱體采用蜂窩結(jié)構(gòu)設(shè)計的通風窗,為元器件進行通風散熱。根據(jù)電子學系統(tǒng)的干擾電磁波波長,在箱壁處開圓孔直徑為5mm,那么對波長小于20mm的電磁波起到完全屏蔽。為了進一步加強屏蔽效果,在箱體內(nèi)壁加一層孔徑為0.5mm的金屬網(wǎng),同時又能達到散熱的目的。把邊界設(shè)置為輻射邊界時,加固箱體距輻射邊界的距離為求解頻率波長的1/4。如圖5所示。仿真求解頻段為0.1 GHz~1GHz;求解步長為0.02GHz;求解迭代步數(shù)為50次;求解精度為0.02。采用離散掃描。首先提取通風板正前方8mm處的泄漏電場的場強值E1;去掉屏蔽殼體后再提取相應(yīng)點的電場場強值E2;對比兩次場強結(jié)果,得到箱體的屏蔽效能
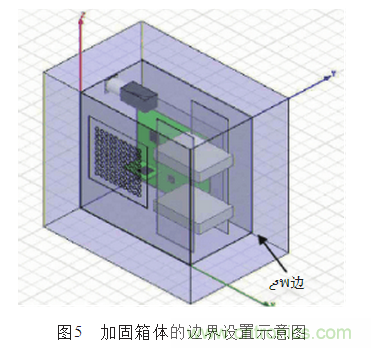
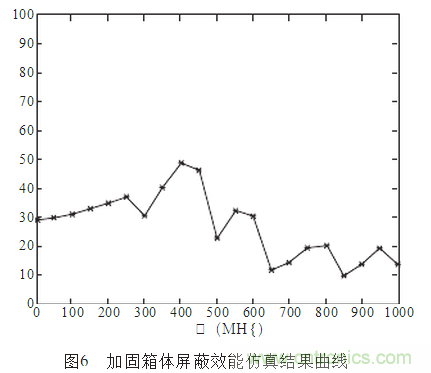
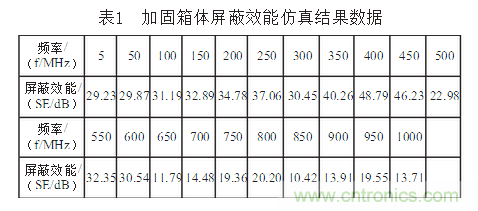
圖6為仿真得到的屏蔽效能曲線。表1為屏蔽效能具體實驗數(shù)據(jù)。
3 EMI測量結(jié)果
3.1 測試框圖
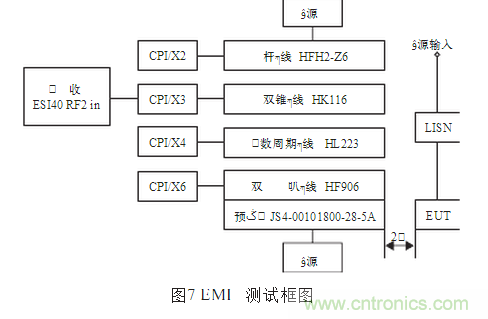
測量來自設(shè)備及其有關(guān)電線、電纜的電場輻射發(fā)射,EMI測試框圖如圖7所示。
3.2 測試過程描述
試樣件放在屏蔽室內(nèi)的測試圓臺上(圓臺上覆有接地銅皮),在距試樣1m處,分別架設(shè)有源棒狀天線(10kHz~30MHz)、雙錐天線(30MHz~200MHz)、對數(shù)周期天線(200MHz~1GHz)和雙脊喇叭天線(1GHz~18GHz),在30MHz~18GHz測試頻段,進行天線的水平極化和垂直極化方式測試。用ESI40接收機監(jiān)測試樣及有關(guān)電纜的電場輻射發(fā)射 。
。
3.3 測試曲線
本實驗是在中國科學院光電研究院EMC實驗室進行,圖8是天線垂直極化狀態(tài)下的電場輻射發(fā)射曲線(10kHz~1GHz),圖9是天線水平極化狀態(tài)下的電場輻射發(fā)射曲線(10kHz~1GHz),圖10是天線水平極化狀態(tài)下的電場輻射發(fā)射曲?線(1GHz~18GHz)。
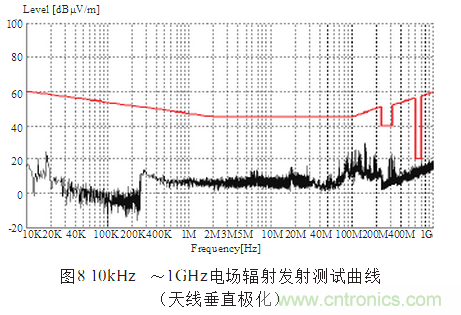
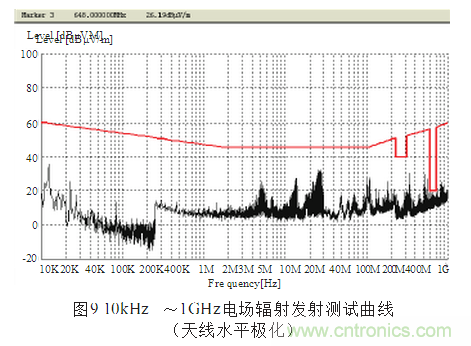
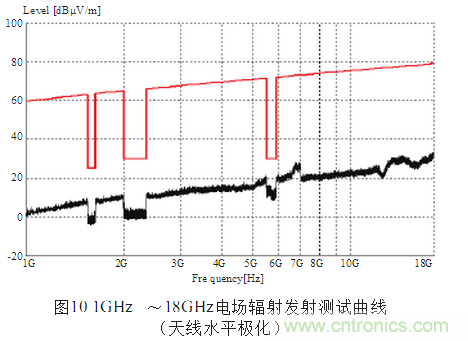
3.4 測試結(jié)果
受試件10kHz~18GHz電場輻射發(fā)射測試,未超過GJB151A-97 RE102限值,該項測試通過。
4 結(jié)論
本文詳細分析設(shè)備的電磁干擾源、結(jié)構(gòu)的縫隙和通孔的影響,選擇合適的屏蔽材料,建立設(shè)備箱體結(jié)構(gòu)模型,仿真實驗得到了設(shè)備較好的屏蔽效能曲線和實驗數(shù)據(jù);并按GJB151A-97要求,對設(shè)備進行EMI輻射測量,實測數(shù)據(jù)未超過GJB151A-97 RE102限值,驗證設(shè)備箱體的EMI屏蔽設(shè)計達到了設(shè)計要求。
參考文獻:
[1] 周旭. 電子設(shè)備防干擾技術(shù)原理與技術(shù)[M]. 北京: 國防工業(yè)出版社, 2005: 33.
[2] 葉志瓊. 電子設(shè)備的電磁兼容技術(shù)[J]. 通信電源技術(shù), 2005, 22(l): 37-40.
[3] 和軍平, 姜建國, 陳斌. 電力電子裝置傳導電磁干擾特性測量的新方法[J]. 電力電子技術(shù), 200l, 5: 32-35.
[4] 盛新慶. 計算電磁學要論[M]. 北京:科學出版社, 2005.
[5] 趙陽, 李世錦, 等. 傳導性EMI噪聲的模態(tài)分離與噪聲抑制問題探討[J]. 南京師范大學學報(工程技術(shù)版), 2004, 4(4): 1-4.
[6] 金建銘. 電磁場有限元方法[M]. 西安: 西安電子科技大學出版社, 1998.
推薦閱讀:






