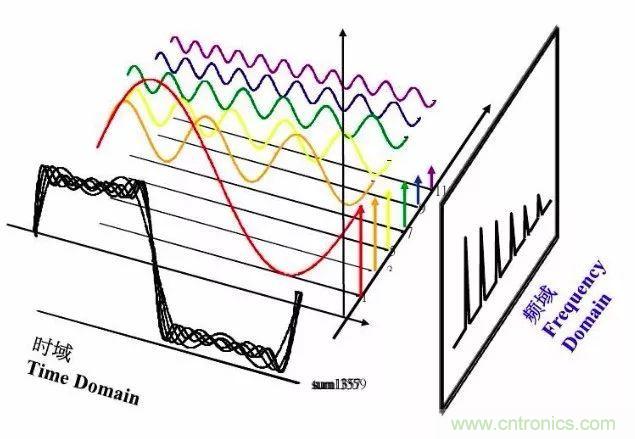
頻域frequency domain 是描述信號(hào)在頻率方面特性時(shí)用到的一種坐標(biāo)系。對任何一個(gè)事物的描述都需要從多個(gè)方面進(jìn)行，每一方面的描述僅為我們認(rèn)識(shí)這個(gè)事物提供部分的信息。例如，眼前有一輛汽車，我可以這樣描述它方面1：顏色，長度，高度。方面2：排量，品牌，價(jià)格。而對于一個(gè)信號(hào)來說，它也有很多方面的特性。如信號(hào)強(qiáng)度隨時(shí)間的變化規(guī)律（時(shí)域特性），信號(hào)是由哪些單一頻率的信號(hào)合成的（頻域特性）

 

時(shí)域time domain

 

在分析研究問題時(shí)，以時(shí)間作基本變量的范圍。

 

時(shí)域是描述數(shù)學(xué)函數(shù)或物理信號(hào)對時(shí)間的關(guān)系。例如一個(gè)信號(hào)的時(shí)域波形可以表達(dá)信號(hào)隨著時(shí)間的變化。

 

若考慮離散時(shí)間，時(shí)域中的函數(shù)或信號(hào)，在各個(gè)離散時(shí)間點(diǎn)的數(shù)值均為已知。若考慮連續(xù)時(shí)間，則函數(shù)或信號(hào)在任意時(shí)間的數(shù)值均為已知。

 

在研究時(shí)域的信號(hào)時(shí)，常會(huì)用示波器將信號(hào)轉(zhuǎn)換為其時(shí)域的波形。

 

時(shí)域是真實(shí)世界，是惟一實(shí)際存在的域。因?yàn)槲覀兊慕?jīng)歷都是在時(shí)域中發(fā)展和驗(yàn)證的，已經(jīng)習(xí)慣于事件按時(shí)間的先后順序地發(fā)生。而評估數(shù)字產(chǎn)品的性能時(shí)，通常在時(shí)域中進(jìn)行分析，因?yàn)楫a(chǎn)品的性能最終就是在時(shí)域中測量的。如下圖2.1所示的時(shí)鐘波形。

 

 

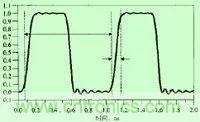
時(shí)鐘波形

 

由上圖可知，時(shí)鐘波形的兩個(gè)重要參數(shù)是時(shí)鐘周期和上升時(shí)間。圖中標(biāo)明了1GHz時(shí)鐘信號(hào)的時(shí)鐘周期和10-90上升時(shí)間。下降時(shí)間一般要比上升時(shí)間短一些，有時(shí)會(huì)出現(xiàn)更多的噪聲。

 

時(shí)鐘周期就是時(shí)鐘循環(huán)重復(fù)一次的時(shí)間間隔，通常用ns度量。時(shí)鐘頻率Fclock，即1秒鐘內(nèi)時(shí)鐘循環(huán)的次數(shù)，是時(shí)鐘周期Tclock的倒數(shù)。

 

Fclock=1/Tclock

 

上升時(shí)間與信號(hào)從低電平跳變到高電平所經(jīng)歷的時(shí)間有關(guān)，通常有兩種定義。一種是10-90上升時(shí)間，指信號(hào)從終值的10%跳變到90%所經(jīng)歷的時(shí)間。這通常是一種默認(rèn)的表達(dá)方式，可以從波形的時(shí)域圖上直接讀出。第二種定義方式是20-80上升時(shí)間，這是指從終值的20%跳變到80%所經(jīng)歷的時(shí)間。

 

時(shí)域波形的下降時(shí)間也有一個(gè)相應(yīng)的值。根據(jù)邏輯系列可知，下降時(shí)間通常要比上升時(shí)間短一些，這是由典型CMOS輸出驅(qū)動(dòng)器的設(shè)計(jì)造成的。在典型的輸出驅(qū)動(dòng)器中，p管和n管在電源軌道Vcc和Vss間是串聯(lián)的，輸出連在這個(gè)兩個(gè)管子的中間。在任一時(shí)間，只有一個(gè)晶體管導(dǎo)通，至于是哪一個(gè)管子導(dǎo)通取決于輸出的高或低狀態(tài)。

 

頻域frequency domain在分析問題時(shí)，以頻率作為基本變量。

 

頻域frequencydomain 是描述信號(hào)在頻率方面特性時(shí)用到的一種坐標(biāo)系。對任何一個(gè)事物的描述都需要從多個(gè)方面進(jìn)行，每一方面的描述僅為我們認(rèn)識(shí)這個(gè)事物提供部分的信息。例如，眼前有一輛汽車，我可以這樣描述它方面1：顏色，長度，高度。方面2：排量，品牌，價(jià)格。而對于一個(gè)信號(hào)來說，它也有很多方面的特性。如信號(hào)強(qiáng)度隨時(shí)間的變化規(guī)律（時(shí)域特性），信號(hào)是由哪些單一頻率的信號(hào)合成的（頻域特性）

 

 

頻域分析

 

頻域（頻率域）——自變量是頻率,即橫軸是頻率,縱軸是該頻率信號(hào)的幅度,也就是通常說的頻譜圖。頻譜圖描述了信號(hào)的頻率結(jié)構(gòu)及頻率與該頻率信號(hào)幅度的關(guān)系。

 

對信號(hào)進(jìn)行時(shí)域分析時(shí)，有時(shí)一些信號(hào)的時(shí)域參數(shù)相同，但并不能說明信號(hào)就完全相同。因?yàn)樾盘?hào)不僅隨時(shí)間變化，還與頻率、相位等信息有關(guān)，這就需要進(jìn)一步分析信號(hào)的頻率結(jié)構(gòu)，并在頻率域中對信號(hào)進(jìn)行描述。動(dòng)態(tài)信號(hào)從時(shí)間域變換到頻率域主要通過傅立葉級數(shù)和傅立葉變換實(shí)現(xiàn)。周期信號(hào)靠傅立葉級數(shù)，非周期信號(hào)靠傅立葉變換。

 

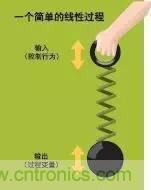
一個(gè)頻域分析的簡例可以通過圖1：一個(gè)簡單線性過程中小孩的玩具來加以說明。該線性系統(tǒng)包含一個(gè)用手柄安裝的彈簧來懸掛的重物。小孩通過上下移動(dòng)手柄來控制重物的位置。

 

任何玩過這種游戲的人都知道，如果或多或少以一種正弦波的方式來移動(dòng)手柄，那么，重物也會(huì)以相同的頻率開始振蕩，盡管此時(shí)重物的振蕩與手柄的移動(dòng)并不同步。只有在彈簧無法充分伸長的情況下，重物與彈簧會(huì)同步運(yùn)動(dòng)且以相對較低的頻率動(dòng)作。

 

隨著頻率愈來愈高，重物振蕩的相位可能更加超前于手柄的相位，也可能更加滯后。在過程對象的固有頻率點(diǎn)上，重物振蕩的高度將達(dá)到最高。過程對象的固有頻率是由重物的質(zhì)量及彈簧的強(qiáng)度系數(shù)來決定的。

 

當(dāng)輸入頻率越來越大于過程對象的固有頻率時(shí)，重物振蕩的幅度將趨于減少，相位將更加滯后（換言之，重物振蕩的幅度將越來越少，而其相位滯后將越來越大）。在極高頻的情況下，重物僅僅輕微移動(dòng)，而與手柄的運(yùn)動(dòng)方向恰恰相反。

 

Bode圖

 

所有的線性過程對象都表現(xiàn)出類似的特性。這些過程對象均將正弦波的輸入轉(zhuǎn)換為同頻率的正弦波的輸出，不同的是，輸出與輸入的振幅和相位有所改變。振幅和相位的變化量的大小取決于過程對象的相位滯后與增益大小。增益可以定義為“經(jīng)由過程對象放大后，輸出正弦波振幅與輸入正弦波振幅之間的比例系數(shù)”，而相位滯后可以定義為“輸出正弦波與輸入正弦波相比較，輸出信號(hào)滯后的度數(shù)”。

 

與穩(wěn)態(tài)增益K值不同的是，“過程對象的增益和相位滯后”將依據(jù)于輸入正弦波信號(hào)的頻率而改變。在上例中，彈簧－重物對象不會(huì)大幅度的改變低頻正弦波輸入信號(hào)的振幅。這就是說，該對象僅有一個(gè)低頻增益系數(shù)。當(dāng)信號(hào)頻率靠近過程對象的固有頻率時(shí)，由于其輸出信號(hào)的振幅要大于輸入信號(hào)的振幅，因此，其增益系數(shù)要大于上述低頻下的系數(shù)。而當(dāng)上例中的玩具被快速搖動(dòng)時(shí)，由于重物幾乎無法起振，因此該過程對象的高頻增益可以認(rèn)為是零。

 

過程對象的相位滯后是一個(gè)例外的因素。由于當(dāng)手柄移動(dòng)得非常慢時(shí)，重物與手柄同步振蕩，所以，在以上的例子中，相位滯后從接近于零的低頻段輸入信號(hào)就開始了。在高頻輸入信號(hào)時(shí)，相位滯后為“-180度”，也就是重物與手柄以相反的方向運(yùn)動(dòng)（因此，我們常常用‘滯后180度’來描述這類兩者反向運(yùn)動(dòng)的狀況）。

 

Bode圖譜表現(xiàn)出彈簧－重物對象在0.01-100弧度/秒的頻率范圍內(nèi)，系統(tǒng)增益與相位滯后的完整頻譜圖。這是Bode圖譜的一個(gè)例子，該圖譜是由貝爾實(shí)驗(yàn)室的Hendrick Bode于1940s年代發(fā)明的一種圖形化的分析工具。利用該工具可以判斷出，當(dāng)以某一特定頻率的正弦波輸入信號(hào)來驅(qū)動(dòng)過程對象時(shí)，其對應(yīng)的輸出信號(hào)的振動(dòng)幅度和相位。欲獲取輸出信號(hào)的振幅，僅僅需要將輸入信號(hào)的振幅乘以“Bode圖中該頻率對應(yīng)的增益系數(shù)”。欲獲取輸出信號(hào)的相位，僅僅需要將輸入信號(hào)的相位加上“Bode圖中該頻率對應(yīng)的相位滯后值”。

 

傅立葉定理

 

在過程對象的Bode圖中表現(xiàn)出來的增益系數(shù)和相位滯后值，反映了系統(tǒng)的非常確定的特征，對于一個(gè)有豐富經(jīng)驗(yàn)的控制工程師而言，該圖譜將其需要知道的、有關(guān)過程對象的一切特性都準(zhǔn)確無誤的告訴了他。由此，控制工程師運(yùn)用此工具，不僅可以預(yù)測“系統(tǒng)未來對于正弦波的控制作用所產(chǎn)生的系統(tǒng)響應(yīng)”，而且能夠知道“系統(tǒng)對任何控制作用所產(chǎn)生的系統(tǒng)響應(yīng)”。

 

傅立葉定理使得以上的分析成為可能，該定理表明任何連續(xù)測量的時(shí)序或信號(hào)，都可以表示為不同頻率的正弦波信號(hào)的無限疊加。數(shù)學(xué)家傅立葉在1822年證明了這個(gè)著名的定理，并創(chuàng)造了為大家熟知的、被稱之為傅立葉變換的算法，該算法利用直接測量到的原始信號(hào)，以累加方式來計(jì)算不同正弦波信號(hào)的頻率、振幅和相位。

 

從理論上說，傅立葉變換和Bode圖可以結(jié)合在一起使用，用以預(yù)測當(dāng)線性過程對象受到控制作用的時(shí)序影響時(shí)產(chǎn)生的反應(yīng)。詳見以下：

 

1）利用傅立葉變換這一數(shù)學(xué)方法，把提供給過程對象的控制作用，從理論上分解為不同的正弦波的信號(hào)組成或者頻譜。

 

2）利用Bode圖可以判斷出，每種正弦波信號(hào)在經(jīng)由過程對象時(shí)發(fā)生了那些變化。換言之，在該圖上可以找到正弦波在每種頻率下的振幅和相位的改變。

 

3）反之，利用反傅立葉變換這一方法，又可以將每個(gè)單獨(dú)改變的正弦波信號(hào)轉(zhuǎn)換成一個(gè)信號(hào)。

 

既然反傅立葉變換從本質(zhì)上說，也是一種累加處理，那么過程對象的線性特征將會(huì)確保－“在第一步中計(jì)算得到的各種理論正弦波”所產(chǎn)生單獨(dú)作用的集合，應(yīng)該等效于“各不同正弦波的累加集合”共同產(chǎn)生的作用。因此，在第三步計(jì)算得到的總信號(hào)，將可以代表“當(dāng)所提供的控制作用輸入到過程對象時(shí)，過程對象的實(shí)際值”。

 

請注意，在以上這些步驟中，沒有哪個(gè)點(diǎn)不是由畫在圖上的控制器產(chǎn)生的單獨(dú)正弦波構(gòu)成。所有這些頻域方面的分析技術(shù)都是概念性的。這是一種方便的數(shù)學(xué)方法，運(yùn)用傅立葉變換（或者緊密相關(guān)的拉普拉斯變換），將時(shí)域信號(hào)轉(zhuǎn)換為頻域信號(hào)，然后再用Bode圖或其他一些頻域分析工具來解決手頭的一些問題，最后再用反傅立葉變換將頻域信號(hào)轉(zhuǎn)換為時(shí)域信號(hào)。

 

絕大多數(shù)可用此方法解決的控制設(shè)計(jì)問題，也可以在時(shí)域內(nèi)通過直接的操控來解決，但是對于計(jì)算而言，利用頻域的方法通常更簡單一些。在上例中，就是用乘法和減法來計(jì)算過程實(shí)際值的頻譜，而該過程實(shí)際值是通過對給定的控制作用進(jìn)行傅立葉變換，爾后又對照Bode圖分析而得到的。

 

 

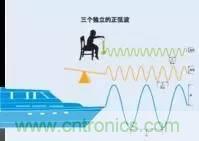
三個(gè)正弦波

 

將所有的正弦波進(jìn)行正確的累加，就會(huì)產(chǎn)生如傅立葉變換所預(yù)示的那類形狀的信號(hào)。當(dāng)有時(shí)這一現(xiàn)象并不直觀，舉個(gè)例子可能有助于理解。

 

請?jiān)俅蜗胂肷厦婺莻€(gè)例子中小孩的重物－彈簧玩具，操場上的蹺蹺板，以及位于外部海洋上的船。設(shè)想這艘船以頻率為w和幅度為A的正弦波形式在海面上起起落落，我們同時(shí)再假設(shè)蹺蹺板也以頻率為3w和幅度為A/3的正弦波形式在振蕩，并且小孩以頻率為5w和幅度為A/5的正弦波形式在搖動(dòng)玩具。‘三張單獨(dú)的正弦波波形圖’已經(jīng)顯示出，如果我們將三個(gè)不同的正弦波運(yùn)動(dòng)進(jìn)行分別觀察的話，每個(gè)正弦波運(yùn)動(dòng)將會(huì)體現(xiàn)出的形式。

 

 

波的疊加

 

現(xiàn)在假設(shè)小孩坐在蹺蹺板上，而蹺蹺板又依次固定在輪船的甲板上。如果這三者單獨(dú)的正弦波運(yùn)動(dòng)又恰巧排列正確的話，那么，玩具所表現(xiàn)出的總體運(yùn)動(dòng)就大約是一個(gè)方波－如圖4：三者合成的正弦波顯示的那樣。

 

以上并非一個(gè)非常確切的實(shí)際例子，但是卻明白無誤的說明：基本頻率正弦波、振幅為三分之一的三倍頻率諧波、以及振幅為五分之一的五倍頻率諧波，它們波形的相加總和大約等于頻率為w、振幅為A的方波。甚至如果再加上振幅為七分之一的七倍頻率諧波、以及振幅為九分之一的九倍頻率諧波時(shí)，總波形會(huì)更像方波。其實(shí)，傅立葉定理早已說明，當(dāng)不同頻率的正弦波以無窮級數(shù)的方式無限累加時(shí)，那么由此產(chǎn)生的總疊加信號(hào)就是一個(gè)嚴(yán)格意義上的、幅度為A的方波。傅立葉定理也可以用來將非周期信號(hào)分解成正弦波信號(hào)的無限疊加。

 

通過求解微分方程分析時(shí)域性能是十分有用的，但對于比較復(fù)雜的系統(tǒng)這種辦法就比較麻煩。因?yàn)槲⒎址匠痰那蠼庥?jì)算工作量將隨著微分方程階數(shù)的增加而增大。另外，當(dāng)方程已經(jīng)求解而系統(tǒng)的響應(yīng)不能滿足技術(shù)要求時(shí)，也不容易確定應(yīng)該如何調(diào)整系統(tǒng)來獲得預(yù)期結(jié)果。從工程角度來看，希望找出一種方法，使之不必求解微分方程就可以預(yù)示出系統(tǒng)的性能。同時(shí)，又能指出如何調(diào)整系統(tǒng)性能技術(shù)指標(biāo)。頻域分析法具有上述特點(diǎn),是研究控制系統(tǒng)的一種經(jīng)典方法,是在頻域內(nèi)應(yīng)用圖解分析法評價(jià)系統(tǒng)性能的一種工程方法。該方法是以輸入信號(hào)的頻率為變量，對系統(tǒng)的性能在頻率域內(nèi)進(jìn)行研究的一種方法。頻率特性可以由微分方程或傳遞函數(shù)求得,還可以用實(shí)驗(yàn)方法測定.頻域分析法不必直接求解系統(tǒng)的微分方程,而是間接地揭示系統(tǒng)的時(shí)域性能,它能方便的顯示出系統(tǒng)參數(shù)對系統(tǒng)性能的影響,并可以進(jìn)一步指明如何設(shè)計(jì)校正.這種分析法有利于系統(tǒng)設(shè)計(jì)，能夠估計(jì)到影響系統(tǒng)性能的頻率范圍。特別地，當(dāng)系統(tǒng)中存在難以用數(shù)學(xué)模型描述的某些元部件時(shí)，可用實(shí)驗(yàn)方法求出系統(tǒng)的頻率特性，從而對系統(tǒng)和元件進(jìn)行準(zhǔn)確而有效的分析。

 

信號(hào)頻域分析

 

是采用傅立葉變換將時(shí)域信號(hào)x(t)變換為頻域信號(hào)X(f)，從而幫助人們從另一個(gè)角度來了解信號(hào)的特征。信號(hào)頻譜X(f)代表了信號(hào)在不同頻率分量成分的大小，能夠提供比時(shí)域信號(hào)波形更直觀，豐富的信息.

 

1822年，法國數(shù)學(xué)家傅里葉(J.Fourier,1768-1830)在研究熱傳導(dǎo)理論時(shí)發(fā)表了“熱的分析理論”，提出并證明了將周期函數(shù)展開為正弦級數(shù)的原理，奠定了傅里葉級數(shù)的理論基礎(chǔ)。

 

泊松(Poisson)、高斯(Guass)等人把這一成果應(yīng)用到電學(xué)中去，得到廣泛應(yīng)用。

 

19世紀(jì)末，人們制造出用于工程實(shí)際的電容器。

 

進(jìn)入20世紀(jì)以后，諧振電路、濾波器、正弦振蕩器等一系列具體問題的解決為正弦函數(shù)與傅里葉分析的進(jìn)一步應(yīng)用開辟了廣闊的前景。

 

在通信與控制系統(tǒng)的理論研究和工程實(shí)際應(yīng)用中，傅里葉變換法具有很多的優(yōu)點(diǎn)。

 

“FFT”快速傅里葉變換為傅里葉分析法賦予了新的生命力。

 

頻域分析是以輸入信號(hào)的頻率為變量，在頻率域，研究系統(tǒng)的結(jié)構(gòu)參數(shù)與性能的關(guān)系, 揭示了信號(hào)內(nèi)在的頻率特性以及信號(hào)時(shí)間特性與其頻率特性之間的密切關(guān)系，從而導(dǎo)出了信號(hào)的頻譜、帶寬以及濾波、調(diào)制和頻分復(fù)用等重要概念。

 

頻域分析的優(yōu)點(diǎn)

 

頻域分析具有明顯的優(yōu)點(diǎn):無需求解微分方程，圖解(頻率特性圖)法,間接揭示系統(tǒng)性能并指明改進(jìn)性能的方向和易于實(shí)驗(yàn)分析.可推廣應(yīng)用于某些非線性系統(tǒng)（如含有延遲環(huán)節(jié)的系統(tǒng)）以及可方便設(shè)計(jì)出能有效抑制噪聲的系統(tǒng)。

 

頻域分析法包括分析系統(tǒng)的

 

1.頻率響應(yīng),它指系統(tǒng)對正弦輸入信號(hào)的穩(wěn)態(tài)響應(yīng)。

 

2.頻率特性,它指系統(tǒng)在不同頻率的正弦信號(hào)輸入時(shí)，其穩(wěn)態(tài)輸出隨頻率而變化(ω由0變到∞)的特性。

 

3.幅頻特性與相頻特性一起構(gòu)成系統(tǒng)的頻率特性。

 

4.幅頻特性,它指的是當(dāng)ω由0到∞變化時(shí)，|G(jω)|的變化特性，記為A(ω)。

 

5.相頻特性, 它指的是當(dāng)ω由0到∞變化時(shí)，∠G(jω)的變化特性稱為相頻特性，記為?(ω)。

 

 

推薦閱讀：